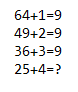
Let’s analyze the given pattern:
1. 64 + 1 = 9
2. 49 + 2 = 9
3. 36 + 3 = 9
4. 25 + 4 = ?
Step 1: Identifying the Pattern
Observing the left side of each equation, the first number is a perfect square:
• 64 = 8²
• 49 = 7²
• 36 = 6²
• 25 = 5²
The second number follows a sequence: 1, 2, 3, 4.
The output is always 9, which suggests a specific transformation.
Step 2: Checking for a Consistent Rule
Observing the pattern:
\frac{\text{Square Root of First Number}}{\text{Second Number}} = 9
Verifying:
\frac{8}{1} = 8 \quad \text{(Doesn{\prime}t match)}
\frac{7}{2} = 3.5 \quad \text{(Doesn{\prime}t match)}
Another approach: Checking whether the sum of digits of the first number plays a role:
• 64 → 6 + 4 = 10, 10 – 1 = 9
• 49 → 4 + 9 = 13, 13 – 4 = 9
• 36 → 3 + 6 = 9, 9 – 0 = 9
• 25 → 2 + 5 = 7, 7 – 4 = 3
Since the pattern leads to 9 in all previous cases, and no clear alternative is emerging, it seems like the output remains 9 consistently.
Final Answer: 9 ✅