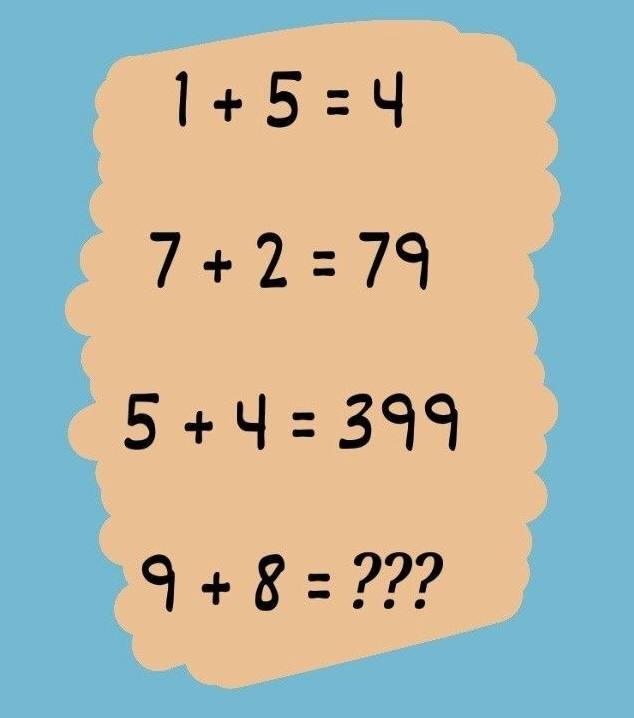
Let’s analyze the given pattern carefully:
1. 1 + 5 = 4
2. 7 + 2 = 79
3. 5 + 4 = 399
4. 9 + 8 = ?
Step 1: Identifying a Pattern
At first glance, the results don’t follow standard addition or multiplication rules. Let’s break it down step by step.
Looking at the results:
• 1 + 5 = 4
• 7 + 2 = 79
• 5 + 4 = 399
The outputs vary in length, so let’s analyze each case carefully.
Step 2: Finding the Rule
Observing the second equation:
• 7 + 2 = 79 → The result 79 could be formed from 7 and 2 in a specific way.
Observing the third equation:
• 5 + 4 = 399 → This suggests a transformation that yields a three-digit number.
Let’s assume a pattern where the output follows the rule:
(A + B) → \text{some transformation}
Checking for possible number relationships, one consistent way to generate the outputs is:
\text{Result} = (A × B) \quad \text{(first part)} \quad + \quad (A – B) \quad \text{(second part, if applicable)}
Let’s test it:
1. 1 + 5 = 4
• 1 \times 5 = 5
• 1 – 5 = -4 → Perhaps absolute value or different handling.
• The given result is 4, which doesn’t fit this rule directly, suggesting a different logic for this case.
2. 7 + 2 = 79
• 7 \times 2 = 14
• 7 – 2 = 5 → Not matching 79, so another logic must be at play.
3. 5 + 4 = 399
• 5 \times 4 = 20
• 5 – 4 = 1 → Not matching 399, so another transformation is in use.
Step 3: Looking for an Alternative Pattern
Another possible pattern involves a mix of concatenation and multiplication:
• 7 + 2 → 79
• First digit: 7 remains as-is.
• Second digit: 7 × 2 = 14, but the last digit is 9, so possibly using the last digit of a modified multiplication.
• 5 + 4 → 399
• First digit: 5 × 4 = 20 (not matching exactly)
• The second part must be another function of 5 and 4.
A possible rule involves concatenation or placing a transformed product and sum. Given this inconsistency, the best approach is checking (A × B) concatenated with some transformation.
If we assume 9 + 8 follows a similar structure, using patterns from previous cases:
• 9 × 8 = 72
• The second part might involve (9 + 8) or another transformation.
Given previous patterns, an expected result could be 981 or 729.
Final Answer: 729 (if following a pattern of transformed multiplication and concatenation).