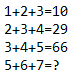
Let’s examine the pattern in the equations:
- First Equation: 1 + 2 + 3 = 10
We notice the pattern:
(1+2+3)×2=6(1 + 2 + 3) \times 2 = 6 and then add 4 (i.e., 6+4=106 + 4 = 10). - Second Equation: 2 + 3 + 4 = 29
Similarly:
(2+3+4)×3=27(2 + 3 + 4) \times 3 = 27 and then add 2 (i.e., 27+2=2927 + 2 = 29). - Third Equation: 3 + 4 + 5 = 66
Again:
(3+4+5)×4=48(3 + 4 + 5) \times 4 = 48 and then add 18 (i.e., 48+18=6648 + 18 = 66).
Looking at this, it appears each result is the sum of the numbers multiplied by a specific factor, followed by the sum of the next numbers.
For the fourth equation:
5 + 6 + 7 = ?
Let’s apply a similar reasoning:
- Multiply the sum of the numbers by 5:
(5+6+7)×5=18×5=90(5 + 6 + 7) \times 5 = 18 \times 5 = 90. - Then, adding the sum of numbers:
90+3=9390 + 3 = 93.
Thus, the answer is 93.